Il rotore è un operatore vettoriale abbastanza utilizzato in analisi che trova una sua modesta applicazione nello studio dei campi come quelli usati per la meccanica dei mezzi fluidi e per la meccanica del continuo. Trattare il rotore nella sua completezza risulta ovviamente molto complesso, ma se ci soffermiamo su alcune sue caratteristiche e su come si rapporta alle altre strutture matematiche si può riuscire ad apprezzare il suo funzionamento. Prima di tutto si definisce come rotore di un campo F la struttura rot(F)=∇xF. L' operatore nabla è invece definito in un riferimento cartesiano tridimensionale i,j,k come ∇=i∂/∂x+j∂/∂x+k∂/∂x. Per il calcolo del rotore si fa riferimento al procedimento del prodotto vettoriale che per un più facile sviluppo viene così schematizzato:
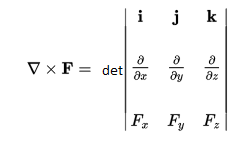
Considerazioni fisico-geometriche:
Una prima considerazione è che essendo un prodotto vettoriale genera un vettore le cui componenti sono sempre ortogonali ad ogni piano considerato (si vede chiaramente che nelle componenti scalari sono chiamate in causa due variabili del campo alla volta,definendo ovviamente un piano di giacitura). Le derivate all'interno dell operatore nabla vanno ad applicarsi ad ogni componente del campo (vedi struttura della matrice) esprimendo un incremento. Come per le funzioni ad una variabile infatti le derivate indicano una pendenza, ovvero una velocità di crescita. Il rotore nel complesso indicherà dunque un incremento del campo nel verso ortogonale alla direzione dello stesso.
Ragioniamo adesso su alcuni fenomeni fisici per capire in effetti come questo operatore non nasca per caso ma sia, come molte definizioni matematiche, costruito ad hoc su fenomeni reali. Immaginiamo questi due campi:

(potremmo associare il primo a quello di un fluido in moto laminare in una condotta e il secondo al moto di un fluido su una lastra che genera taglio oppure un tornado che si avvita su un asse)
Si vede subito che le linee del primo campo sono tutte parallele tra di loro e che un rotore applicato ad esso darebbe valore nullo (nessuna variazione dell intensità del campo ortogonalmente ad esso).
Se invece prendiamo ad esame il secondo campo la variazione di intensità ortogonale genererà appunto un rotore non nullo. Dal punto di vista fisico infatti il rotore sta ad intendere una vorticosità, ovvero una rotazione intorno ad un asse sul quale giace proprio lo stesso rotore [N.B.=il rotore di un campo vettoriale è un vettore,in conformità alla natura del prodotto vettoriale]
Approfondimento: rotore di un tensore
Approfondimento: rotore della divergenza
Approfondimento: rotore di un campo conservativo
Approfondimento: teorema di Stokes (solo enunciato)
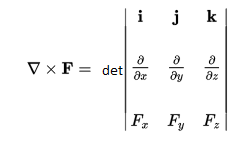
Una prima considerazione è che essendo un prodotto vettoriale genera un vettore le cui componenti sono sempre ortogonali ad ogni piano considerato (si vede chiaramente che nelle componenti scalari sono chiamate in causa due variabili del campo alla volta,definendo ovviamente un piano di giacitura). Le derivate all'interno dell operatore nabla vanno ad applicarsi ad ogni componente del campo (vedi struttura della matrice) esprimendo un incremento. Come per le funzioni ad una variabile infatti le derivate indicano una pendenza, ovvero una velocità di crescita. Il rotore nel complesso indicherà dunque un incremento del campo nel verso ortogonale alla direzione dello stesso.
Ragioniamo adesso su alcuni fenomeni fisici per capire in effetti come questo operatore non nasca per caso ma sia, come molte definizioni matematiche, costruito ad hoc su fenomeni reali. Immaginiamo questi due campi:

Si vede subito che le linee del primo campo sono tutte parallele tra di loro e che un rotore applicato ad esso darebbe valore nullo (nessuna variazione dell intensità del campo ortogonalmente ad esso).
Se invece prendiamo ad esame il secondo campo la variazione di intensità ortogonale genererà appunto un rotore non nullo. Dal punto di vista fisico infatti il rotore sta ad intendere una vorticosità, ovvero una rotazione intorno ad un asse sul quale giace proprio lo stesso rotore [N.B.=il rotore di un campo vettoriale è un vettore,in conformità alla natura del prodotto vettoriale]
Approfondimento: rotore di un tensore
Approfondimento: rotore della divergenza
Approfondimento: rotore di un campo conservativo
Approfondimento: teorema di Stokes (solo enunciato)
Commenti
Posta un commento